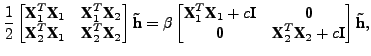

Next: Kernel CCA for Wiener
Up: Measures Against Overfitting
Previous: Order Reduction
Regularization
A second method considers regularizing the
solution by adding a normalization restriction to the norm of
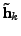 [11,12] or
[11,12] or
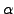
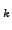 [21]. Here, we apply the classical
regularization technique in the framework of LS regression, which
yields the following CCA-GEV problem
[21]. Here, we apply the classical
regularization technique in the framework of LS regression, which
yields the following CCA-GEV problem
or, in the case of K-CCA
Therefore, the regularized version of CCA (or K-CCA) can be
reformulated as two coupled LS (or kernel-LS) regression problems.
Steven Van Vaerenbergh
Last modified: 2006-04-05