

Next: The Online Algorithm
Up: Least-Squares Regression
Previous: Kernel Methods
For most useful kernel functions, the dimension of the feature
space, 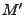 , will be much higher than the number of available data
points
, will be much higher than the number of available data
points  (for instance, in case the Gaussian kernel is used the
feature space will have dimension
(for instance, in case the Gaussian kernel is used the
feature space will have dimension
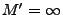 ). In these cases,
Eq. (5) could have an infinite number of solutions,
representing an overfit problem.
). In these cases,
Eq. (5) could have an infinite number of solutions,
representing an overfit problem.
Various techniques to handle this overfitting have been presented.
One possible method is to reduce the order of the feature space
[6,4,5]. A second
method, used here, is to regularize the solution. More
specifically, the norm of the solution
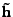 is penalized
to obtain the following problem:
is penalized
to obtain the following problem:
whose solution is given by
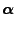 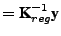 |
(9) |
with
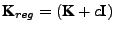 ,
,
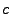 a regularization constant and
a regularization constant and
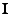 the identity
matrix.
the identity
matrix.
 Pdf version (187 KB)
Pdf version (187 KB)
Steven Van Vaerenbergh
Last modified: 2006-03-08
![]() is penalized
to obtain the following problem:
is penalized
to obtain the following problem:
 Pdf version (187 KB)
Pdf version (187 KB)