Kernel Methods

Kernel methods are powerful nonlinear techniques based on a nonlinear transformation of the data ${\mathbf x}_i$ into a high-dimensional feature space, in which it is more likely that the transformed data $\Phi({\mathbf x}_i)$ is linearly separable. In feature space, inner products can be calculated by using a positive definite kernel function satisfying Mercer's condition [14]: $\kappa({\mathbf x}_i, {\mathbf x}_j) = \langle \Phi({\mathbf x}_i), \Phi({\mathbf x}_j) \rangle$. This simple and elegant idea, also known as the ``kernel trick'', allows to perform inner-product based algorithms implicitly in feature space by replacing all inner products by kernels. A commonly used kernel function is the Gaussian kernel

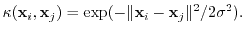$$\kappa({\mathbf x}_i,{\mathbf x}_j) = \exp(-\Vert{\mathbf x}_i-{\mathbf x}_j\Vert^2/2\sigma^2).$$ (1)

In kernel-based regression techniques, a nonlinear mapping is evaluated as a linear combination of kernels of support vectors ${\mathbf x}_i$

$$f({\mathbf x}) = \sum_{i=1}^N \alpha_i \kappa({\mathbf x}_i,{\mathbf x}) .$$ (2)

Thanks to the Representer Theorem [1], the nonlinearity $f$ can be represented sufficiently well by choosing the training vectors as the support of this expansion.