Adding a row and column to the kernel matrix

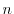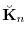In the $n$-th iteration, a new pattern $({\mathbf x}_n,y_n)$ is first added to the memory, which corresponds to adding one row and one column to the kernel matrix ${\mathbf K}_{n-1}$. We call this operation ``upsizing'' the matrix, and the result is denoted as $\breve{{\mathbf K}}_{n}$. Given the inverse matrix ${\mathbf K}_{n-1}^{-1}$, the inverse of the upsized matrix, $\breve{{\mathbf K}}_{n}^{-1}$, can be obtained by calculating

$$\breve{{\mathbf K}}_{n} = \begin{bmatrix}{\mathbf K}_{n-1} & \tex... ... g{\mathbf e}{\mathbf e}^T & -g{\mathbf e} -g{\mathbf e}^T & g \end{bmatrix},$$ (5)

in which 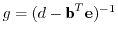${\mathbf e}= {\mathbf K}_{n-1}^{-1}{\mathbf b}$, $g = (d - \textbf{b}^T{\mathbf e})^{-1}$, and ${\mathbf b}$ and $d$ contain kernels between ${\mathbf x}_n$ and the other points in memory (see [12]).