

Next: Conclusions
Up: Simulation Results
Previous: Static Wiener System
A third setup is presented to test the tracking capability of the
online K-CCA algorithm. The analyzed Wiener system has a minimum
phase linear filter whose coefficients change linearly from
 to
to
 over
over  input
samples, and nonlinearity
input
samples, and nonlinearity
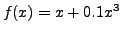 . The input signal is
a white zero-mean Gaussian with unit variance and additive white
Gaussian noise with zero-mean is added to the output, matching an
SNR of
. The input signal is
a white zero-mean Gaussian with unit variance and additive white
Gaussian noise with zero-mean is added to the output, matching an
SNR of 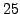 dB. The online K-CCA algorithm is applied with
dB. The online K-CCA algorithm is applied with  .
As an example we present the evolution of the third coefficient of
.
As an example we present the evolution of the third coefficient of
 compared to the third coefficient of
compared to the third coefficient of  (see Fig.
9). After an initialization period of length
(see Fig.
9). After an initialization period of length
 in which the initialization data in the kernel matrix are
replaced by real data, it can be observed that the algorithm is
capable of functioning in a time-varying environment.
in which the initialization data in the kernel matrix are
replaced by real data, it can be observed that the algorithm is
capable of functioning in a time-varying environment.
Figure 9:
Tracking capability of the online K-CCA algorithm. The
dotted line represents a coefficient of the linear filter of a
time-varying Wiener system. The straight line represents the
estimated filter coefficient.
|
|


Next: Conclusions
Up: Simulation Results
Previous: Static Wiener System
Steven Van Vaerenbergh
Last modified: 2006-04-05

