Post-nonlinear mixture model

In a realistic scenario the $m$ sensors that measure the mixtures show some kind of nonlinearity, which suggests the extension of (2) to a post-nonlinear mixture model

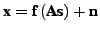$$\textbf{x} = \textbf{f}\left(\textbf{A}\textbf{s}\right) + \textbf{n}$$ (3)

where $\textbf{f}(\cdot) = [f_1(\cdot), f_2(\cdot), \dots, f_m(\cdot) ]^T$ is a componentwise nonlinear function and $\textbf{x} \in \mathbb{R}^{m\times 1}$ is the measurement random vector. For the underdetermined case ($m < n$) the methods from linear BSS are not able to estimate the sources properly. A scatter plot example of PNL mixtures is shown in Fig. 2(b).

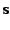The proposed algorithm aims at estimating the inverse nonlinearities $\textbf{g} = \textbf{f}^{-1}$, under the condition that they are invertible and linear for small input values. This leads directly to an estimate of the linear mixtures $\textbf{y} = \textbf{g}\left(\textbf{x}\right)$, which can be used to recover the original sources $\textbf{s}$ relying on known methods for underdetermined linear BSS.