Discarding criterion

In the 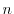$n$-th iteration, the pattern $({\mathbf x}_n,y_n)$ is first added to the memory, which now contains $M+1$ patterns. The inverse kernel matrix is updated as described in section 3.1.1, and the regression coefficients $\alpha_i$ can be recalculated according to (4). In this section we discuss a criterion that determines the least significant of the $M+1$ stored patterns. Once it is found, the kernel matrix is downsized as in Alg. 1, and $\alpha_i$ is recalculated through (4).

Ideally, the pruning criterion should take into account the information present in the stored input data ${\mathbf x}_i$ and the stored labels $y_i$. A simple criterion consists in selecting the pattern that bears least error after it is omitted. As shown in [7], this error can be obtained as

$$d({\mathbf x}_i,y_i) = \frac{\vert\alpha_i\vert}{[\breve{{\mathbf K}}_n^{-1}]_{i,i}},$$ (8)

which is easily found since 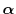$\vec{\alpha}$ and $\breve{{\mathbf K}}_n^{-1}$ have been calculated previously. Moreover, experiments in [7,8] show that this criterion obtains significant better performance than various related criteria.