Phase 1: Grouping of symmetric clusters.
Spectral clustering is extended to find clusters consisting of two
symmetric clusters at a time. Consider the distance measure
![$\displaystyle d(\textbf{x}[i],\textbf{x}[j]) = \min \left( \left\vert
\textbf{...
...ert^2, \left\vert
\textbf{x}^{+}[i] - \textbf{x}^{-}[j] \right\vert^2 \right),$](img76.png) |
(7) |
where
![$ \textbf{x}^{-}[j] = [-\textbf{x}[j]^T, t[j]^T ]^T$](img77.png) is the
point symmetric to
is the
point symmetric to
![$ \textbf{x}^{+}[j]$](img78.png) . As can be seen, this measure
is small in two cases: Firstly for points that are very close to
each other, and secondly for points that are very close to opposite
of each other. If the the modified Gaussian kernel
(4) is used with this distance measure for
spectral clustering, neighboring points as well as opposite points
will be grouped together, leading to
. As can be seen, this measure
is small in two cases: Firstly for points that are very close to
each other, and secondly for points that are very close to opposite
of each other. If the the modified Gaussian kernel
(4) is used with this distance measure for
spectral clustering, neighboring points as well as opposite points
will be grouped together, leading to 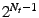 clusters. This
first phase avoids the incorrect clustering that might occur when
some of the threads have a low number of data points, by combining
the information of symmetric threads.
clusters. This
first phase avoids the incorrect clustering that might occur when
some of the threads have a low number of data points, by combining
the information of symmetric threads.
Steven Van Vaerenbergh
Last modified: 2007-10-17