Clustering procedure for
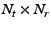 BPSK MIMO systems
BPSK MIMO systems
The geometrical property indicated in the
previous section is not limited to
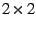 systems. In a
general
systems. In a
general
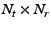 BPSK MIMO system with fast time-varying
channels, for any cluster following a certain trajectory in time,
there is always another cluster following the symmetric trajectory.
Combining the data of two such clusters might provide a more robust
clustering problem. This observation leads to the following
two-phase algorithm: In the first phase, groups of symmetric
clusters are detected. One clustering problem needs to be solved
here to find
BPSK MIMO system with fast time-varying
channels, for any cluster following a certain trajectory in time,
there is always another cluster following the symmetric trajectory.
Combining the data of two such clusters might provide a more robust
clustering problem. This observation leads to the following
two-phase algorithm: In the first phase, groups of symmetric
clusters are detected. One clustering problem needs to be solved
here to find 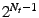 clusters. In the second phase, each group
of symmetric clusters is separated into two different clusters,
representing
clusters. In the second phase, each group
of symmetric clusters is separated into two different clusters,
representing  independent problems.
independent problems.
Subsections
Steven Van Vaerenbergh
Last modified: 2007-10-17