Example: $2 \times 2$ BPSK MIMO

In the noiseless case ( $\textbf{v}[n] = \textbf{0}$ ), Eq. (1) can be written as

$$\textbf{x}[n] = \textbf{H}[n] \textbf{d}[n]$$ (6)

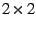For a $2 \times 2$ BPSK MIMO system, there will be $4$ symbol clusters to detect in the data $\textbf{x}[n]$ , corresponding to the transmitted symbol vectors $[+1,+1]$ , $[+1,-1]$ , $[-1,-1]$ and $[-1,-1]$ . In Fig. 1 and Fig. 3 we can observe that for any cluster following a certain trajectory, there is always another cluster following a trajectory symmetric with respect to the origin. This observation is confirmed by (6): since a BPSK system can emit both $\textbf{d}[n]$ and $-\textbf{d}[n]$ , the data point $\textbf{x}[n]$ as well as its opposite $-\textbf{x}[n]$ can be received. These data points lie in clusters that follow symmetric trajectories. This property can be exploited to improve the spectral clustering stage, by first grouping together the data points that follow symmetric trajectories, as will be shown in Section 4.2. Although this work is limited to BPSK systems, the extension of the described property and procedure to other $M$ -PSK constellations is straightforward.