

Next: Kernel Canonical Correlation Analysis
Up: CCA and Kernel CCA
Previous: CCA and Kernel CCA
Canonical Correlation Analysis
Given two full-rank data matrices
 and
and
 ,
canonical correlation analysis (CCA) is defined as the problem of
finding two canonical vectors
,
canonical correlation analysis (CCA) is defined as the problem of
finding two canonical vectors
 and
and
 that
maximize the correlation between the canonical variates
that
maximize the correlation between the canonical variates
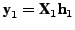 and
and
 , i.e.
, i.e.
 |
(1) |
or equivalently
where
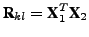 is an
estimate of the cross-correlation matrix. An alternative
formulation of CCA into the framework of least squares (LS)
regression has been proposed in
[16,17]. Specifically, it has
been proved that CCA can be reformulated as the problem of
minimizing
is an
estimate of the cross-correlation matrix. An alternative
formulation of CCA into the framework of least squares (LS)
regression has been proposed in
[16,17]. Specifically, it has
been proved that CCA can be reformulated as the problem of
minimizing
 |
(2) |
and solving (1) or (2) by the
method of Lagrange multipliers, CCA can be rewritten as the
following generalized eigenvalue (GEV) problem
 |
(3) |
where
![$ \textbf{h} = [\textbf{h}_1^T \textbf{h}_2^T]^T$](img30.png) , and
, and
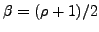 is a parameter related to a principal component
analysis (PCA) interpretation of CCA [17].
is a parameter related to a principal component
analysis (PCA) interpretation of CCA [17].
The solution of (3) can be directly obtained
applying standard GEV algorithms. However, the special structure
of the CCA problem has been recently exploited to obtain efficient
CCA algorithms
[16,17,18].
Specifically, denoting the pseudoinverse of
 as
as
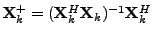 , the GEV problem (3) can
be viewed as two coupled LS regression problems
, the GEV problem (3) can
be viewed as two coupled LS regression problems
where
 . This idea has been used in
[16,17] to develop an algorithm
based on the solution of these regression problems iteratively: at
each iteration
. This idea has been used in
[16,17] to develop an algorithm
based on the solution of these regression problems iteratively: at
each iteration  two LS regression problems are solved using
two LS regression problems are solved using
as desired output. Furthermore, this LS regression framework has
been exploited to develop adaptive CCA algorithms based on the
recursive least-squares algorithm (RLS)
[16,17].


Next: Kernel Canonical Correlation Analysis
Up: CCA and Kernel CCA
Previous: CCA and Kernel CCA
Steven Van Vaerenbergh
Last modified: 2006-04-05
![]() and
and
![]() ,
canonical correlation analysis (CCA) is defined as the problem of
finding two canonical vectors
,
canonical correlation analysis (CCA) is defined as the problem of
finding two canonical vectors
![]() and
and
![]() that
maximize the correlation between the canonical variates
that
maximize the correlation between the canonical variates
![]() and
and
![]() , i.e.
, i.e.
![]() as
as
![]() , the GEV problem (3) can
be viewed as two coupled LS regression problems
, the GEV problem (3) can
be viewed as two coupled LS regression problems
