

Next: Online Algorithm
Up: Online Kernel Canonical Correlation
Previous: Regularization
Kernel CCA for Wiener Systems
Figure 1:
A nonlinear Wiener system.
|
|
A Wiener system is a well-known and simple nonlinear system which
consists of a cascade of a linear dynamic system and a memoryless
nonlinearity (see Fig. 1). Such a nonlinear
channel is encountered frequently, e.g. in digital satellite
communications [22] or in digital magnetic recording
[23]. Traditionally the problem of nonlinear
equalization or identification has been tackled by considering
nonlinear structures such as multilayer perceptrons (MLPs)
[24], recurrent neural networks [25] or
piecewise linear networks [26]. Most of the proposed
techniques treated the Wiener system as a black-box, although use
can be made of its simple structure.
Recently a supervised identification setup for Wiener systems was
presented [6] that exploits the
cascade structure by introducing joint identification of the
linear filter and the inverse nonlinearity, as in Fig.
2. The estimator models for linear
filter and nonlinearity are adjusted by minimizing the error
between their outputs ![$ y_1[n]$](img86.png) and
and ![$ y_2[n]$](img4.png) . By doing so,
. By doing so,
 will represent an estimator of
will represent an estimator of  , while
, while  will represent
will represent 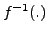 in the noiseless case, assuming that
in the noiseless case, assuming that
 is invertible in the output data range.
is invertible in the output data range.
Figure 2:
The used Wiener system identification diagram.
|
|
To avoid the trivial zero solution or divergence of the
estimators, a restriction should be taken into account for this
approach to work. The two most obvious options are imposing
restrictions on
- the norm of the estimator coefficients
- the norm of the signals
![$ y_1[n]$](img86.png) and
and ![$ y_2[n]$](img4.png) .
.
The first type of restriction was used in
[6]. Interestingly, the second type
is a direct application of (kernel) CCA, as can be seen from Eq.
(2). K-CCA can be applied to this problem by
maximizing the correlation between the linear projection ![$ y_1[n]$](img86.png) (linear kernel,
(linear kernel,
 ) of the system input
) of the system input ![$ x_1[n]$](img1.png) and the
nonlinear projection
and the
nonlinear projection ![$ y_2[n]$](img4.png) (gaussian or other nonlinear kernel)
of the system output
(gaussian or other nonlinear kernel)
of the system output ![$ x_2[n]$](img2.png) . To prevent overfitting, the
nonlinear kernel matrix is regularized as mentioned in Section
II-C. However, regularization is not needed for the
linear kernel, since the feature space of a linear kernel is the
original data space, with dimension
. To prevent overfitting, the
nonlinear kernel matrix is regularized as mentioned in Section
II-C. However, regularization is not needed for the
linear kernel, since the feature space of a linear kernel is the
original data space, with dimension  . Using this insight
the linear kernel matrix can be replaced by an estimate of the
correlation matrix, as shown below. Starting from the general form
of the GEV problem (7)
. Using this insight
the linear kernel matrix can be replaced by an estimate of the
correlation matrix, as shown below. Starting from the general form
of the GEV problem (7)
 |
(8) |
and substituting
 and
and

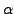
 ,
(8) is equivalent to solving
,
(8) is equivalent to solving
where
 represents the solution to the primal
problem, for the linear part, and
represents the solution to the primal
problem, for the linear part, and
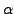
 represents
the solution to the dual problem, for the nonlinear part.
Substituting
represents
the solution to the dual problem, for the nonlinear part.
Substituting

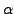
 , this GEV constitutes two coupled
LS regression problems:
, this GEV constitutes two coupled
LS regression problems:
 |
(9) |


Next: Online Algorithm
Up: Online Kernel Canonical Correlation
Previous: Regularization
Steven Van Vaerenbergh
Last modified: 2006-04-05

![]() and
and ![]() . By doing so,
. By doing so,
![]() will represent an estimator of
will represent an estimator of ![]() , while
, while ![]() will represent
will represent ![]() in the noiseless case, assuming that
in the noiseless case, assuming that
![]() is invertible in the output data range.
is invertible in the output data range.