Bayesian model

In a Bayesian setting, we need a model that describes the observations, and priors on the parameters of such model. Following the standard setup of GP regression, we can describe observations as the sum of an unobservable latent function of the inputs plus zero-mean Gaussian noise

$$y_i = f({\boldsymbol{\mathbf{x}}}_i) + \varepsilon_i.$$ (1)

In order to perform Bayesian inference, we also need a prior over the latent function, which is taken to be a zero-mean GP with covariance function $k({\boldsymbol{\mathbf{x}}},{\boldsymbol{\mathbf{x}}}')$. The use of a GP prior has a simple meaning: It implies that the prior joint distribution of vector ${\boldsymbol{\mathbf{f}}}_t = [f_1,\ldots, f_t]^\top$ (where $f_i = f({\boldsymbol{\mathbf{x}}}_i)$) is a zero-mean multivariate Gaussian with covariance matrix ${\boldsymbol{\mathbf{K}}}_t$, with elements $[{\boldsymbol{\mathbf{K}}}_t]_{ij} = k({\boldsymbol{\mathbf{x}}}_i,{\boldsymbol{\mathbf{x}}}_j)$. In line with the previous literature on KRLS, we will refer to $k({\boldsymbol{\mathbf{x}}},{\boldsymbol{\mathbf{x}}}')$ as the kernel function, and to ${\boldsymbol{\mathbf{K}}}_t$ as the kernel matrix (which in this example would correspond to inputs $\{{\boldsymbol{\mathbf{x}}}_1,\ldots,{\boldsymbol{\mathbf{x}}}_t\}$). 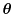For the sake of clarity, in the following we will omit conditioning on the inputs $\{{\boldsymbol{\mathbf{x}}}_i\}_{i=1}^t$ or the parameters ${\boldsymbol{\mathbf{\theta}}}$ that parameterize the kernel function.