

Next: Preprocessing
Up: Dividing the samples into
Previous: Dividing the samples into
Spectral clustering [17] is a technique that
clusters points based on a spectral analysis of the matrix of
point-to-point similarities. This ``affinity'' matrix is formed as
 where
where
 is some distance measure between
points
is some distance measure between
points
 and
and
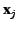 and
and  is a scaling
constant. Spectral clustering obtains good clustering performance
in cases where classic methods such as k-means fail, for instance
when one data set is surrounded by another one. Nevertheless, its
efficiency depends on the choice of
is a scaling
constant. Spectral clustering obtains good clustering performance
in cases where classic methods such as k-means fail, for instance
when one data set is surrounded by another one. Nevertheless, its
efficiency depends on the choice of  . In addition, since
it requires obtaining the eigenvectors of an
. In addition, since
it requires obtaining the eigenvectors of an  matrix,
care should be taken to reduce the computational cost when the
number of samples
matrix,
care should be taken to reduce the computational cost when the
number of samples  is large.
is large.
In [18], Zelnik-Manor and Perona proposed to
calculate the affinity matrix as
 where
the ``local scale''
where
the ``local scale''
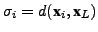 is
the distance between
is
the distance between
 and its
and its 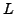 -th neighbor, with
-th neighbor, with
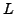 constant and depending on the data dimension. This has certain
advantages over the original spectral clustering. Firstly, the
results do not depend on the choice of
constant and depending on the data dimension. This has certain
advantages over the original spectral clustering. Firstly, the
results do not depend on the choice of  . Secondly, in the
context of the underdetermined PNL BSS problem points with a
higher local scale will likely correspond to multiple active
sources, since the local scale is inversely proportional to the
local density of points (see Fig. 2(a) and (b)).
. Secondly, in the
context of the underdetermined PNL BSS problem points with a
higher local scale will likely correspond to multiple active
sources, since the local scale is inversely proportional to the
local density of points (see Fig. 2(a) and (b)).


Next: Preprocessing
Up: Dividing the samples into
Previous: Dividing the samples into
Steven Van Vaerenbergh
Last modified: 2006-04-05
![]() where
the ``local scale''
where
the ``local scale''
![]() is
the distance between
is
the distance between
![]() and its
and its ![]() -th neighbor, with
-th neighbor, with
![]() constant and depending on the data dimension. This has certain
advantages over the original spectral clustering. Firstly, the
results do not depend on the choice of
constant and depending on the data dimension. This has certain
advantages over the original spectral clustering. Firstly, the
results do not depend on the choice of ![]() . Secondly, in the
context of the underdetermined PNL BSS problem points with a
higher local scale will likely correspond to multiple active
sources, since the local scale is inversely proportional to the
local density of points (see Fig. 2(a) and (b)).
. Secondly, in the
context of the underdetermined PNL BSS problem points with a
higher local scale will likely correspond to multiple active
sources, since the local scale is inversely proportional to the
local density of points (see Fig. 2(a) and (b)).