

Next: Removing the first row
Up: Matrix inversion formulas
Previous: Matrix inversion formulas
Adding a row and a column
To a given non-singular matrix
 a row and column are added as shown below, resulting
in matrix
a row and column are added as shown below, resulting
in matrix
 . The inverse matrix
. The inverse matrix
 can
then be expressed in terms of the known elements and
can
then be expressed in terms of the known elements and
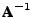 as follows:
as follows:
 |
(11) |
with
 .
.
 Pdf version (187 KB)
Pdf version (187 KB)
Steven Van Vaerenbergh
Last modified: 2006-03-08


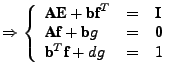
 Pdf version (187 KB)
Pdf version (187 KB)