

Next: Measures Against Overfitting
Up: Least-Squares Regression
Previous: Linear Methods
The linear LS methods can be extended to nonlinear versions by
transforming the data into a feature space. Using the transformed
vector
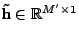 and the
transformed data matrix
and the
transformed data matrix
 , the LS problem (2) can be written in feature space
as
, the LS problem (2) can be written in feature space
as
 |
(3) |
The transformed solution
 can now also be
represented in the basis defined by the rows of the (transformed)
data matrix
can now also be
represented in the basis defined by the rows of the (transformed)
data matrix
 , namely as
, namely as
Moreover, introducing the kernel matrix
 the LS problem in feature space
(3) can be rewritten as
the LS problem in feature space
(3) can be rewritten as
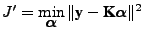 |
(5) |
in which the solution
 is an
is an  vector.
The advantage of writing the nonlinear LS problem in the dual
notation is that thanks to the ``kernel trick'', we only need to
compute
vector.
The advantage of writing the nonlinear LS problem in the dual
notation is that thanks to the ``kernel trick'', we only need to
compute
 , which is done as
, which is done as
 |
(6) |
where
 and
and
 are the
are the 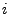 -th and
-th and  -th
rows of
-th
rows of
 . As a consequence the computational
complexity of operating in this high-dimensional space is not
necessarily larger than that of working in the original
low-dimensional space.
. As a consequence the computational
complexity of operating in this high-dimensional space is not
necessarily larger than that of working in the original
low-dimensional space.


Next: Measures Against Overfitting
Up: Least-Squares Regression
Previous: Linear Methods
 Pdf version (187 KB)
Pdf version (187 KB)
Steven Van Vaerenbergh
Last modified: 2006-03-08
 Pdf version (187 KB)
Pdf version (187 KB)