Linear Methods

The least-squares (LS) criterion [8] is a widely used method in signal processing. Given a vector 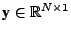$\textbf{y} \in \mathbb{R}^{N\times 1}$ and a data matrix $\textbf{X} \in \mathbb{R}^{N\times M}$ of observations, it consists in seeking the optimal vector $\textbf{h} \in \mathbb{R}^{M\times 1}$ that solves

$$J = \min_{\textbf{h}} \Vert\textbf{y} - \textbf{X}\textbf{h}\Vert^2.$$ (2)

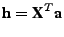It should be clear that the solution $\textbf{h}$ can be represented in the basis defined by the rows of $\textbf{X}$. Hence it can also be written as $\textbf{h} = \textbf{X}^T\textbf{a}$, making it a linear combination of the input patterns (this is sometimes denoted as the ``dual representation'').

For many problems however, not all data are known in advance and the solution has to be re-calculated as the new observations become available. An online algorithm is then needed, which in case of linear problems is given by the well-known recursive least-squares (RLS) algorithm [8].